Золотое сечение в музыке. Музыка золотого сечения полный сеанс.

Золотое сечение в музыке. Музыка золотого сечения полный сеанс.

Обретение внутренней гармонии.

Великий Пифагор создал тайную школу, где изучалась мистическая суть "Золотого Сечения". Евклид применил его, создавая свою геометрию, а фидий - свои бессмертные скульптуры. Платон рассказывал, что вселенная устроена согласно "Золотому Сечению". Высшую гармонию "Золотого Сечения" будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и "золотое сечение" - это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы "Золотого Сечения", спасаясь от дьявола.
Эта божественная пропорция мистическим образом всему живому сопутствует. Неживая природа не знает, что такое "Золотое Сечение".
Только в том случае, если говорить про музыку, то золотая пропорция является критерием гармонии композиции музыкального произведения.
Музыка создана по принципу золотого сечения оказывает целительное и гармоничное воздействие на поля живого поля.
Прослушивая такую музыку вы будете испытывать одухотворение, любовь, восстановление физического состояния. Автор музыки: Веретенников Сергей.

Связанные вопросы и ответы:

Золотое сечение в современной музыке. Метод золотого сечения в музыкальных произведениях

«Золотое сечение» – это понятие, скорее, математическое и его изучение – задача науки. Это деление некоей величины на две части в таком отношении, когда болььшая часть так будет относиться к меньшей, как целое к большей. Данное отношение оказывается равным трансцендентному числу Ф=1,6180339… с удивительными свойствами.

Метод золотого сечения — это поиск значений функции на заданном отрезке. Данный метод основывается на принципе деления отрезка в так называемой золотой пропорции. Наибольшее распространение он получил для поиска экстремальных значений при решении задач, связанных с оптимизацией. Кроме математики, метод золотого сечения используется в самых разных сферах, начиная от архитектуры, искусства и заканчивая астрономией. Так, например, известный советский режиссёр Сергей Эйзенштейн использовал его в своей картине «Броненосец Потёмкин», а Леонардо да Винчи – при написании им знаменитой «Джоконды».

Метод золотого сечения применяется и в музыке. Оказалось, что в музыкальных произведениях очень часто встречается эта золотая пропорция. В начале 20 века на заседании Московского музыкального кружка было сделано сообщение, содержащее информацию о том, какое применение находит золотое сечение в музыке. Сообщение с огромным интересом слушали члены музыкального кружка композиторы С. Рахманинов, С. Танеев, Р. Глиэр и другие. Доклад музыковеда Розенова Э.К. «Закон золотого сечения в музыке и поэзии» положил начало исследованиям математических закономерностей, связанных с золотой пропорцией, в музыке. Он проанализировал музыкальные произведения Моцарта, Баха, Бетховена, Вагнера, Шопена, Глинки и других композиторов и показал, что в их произведениях присутствует эта «божественная пропорция».

Кульминация многих музыкальных произведений располагается не в центре, а немного смещена к концу произведения в соотношении 62:38 – это и есть точка золотой пропорции. Доктор искусствоведения, профессор Л. Мазель заметил, изучая восьмитактные мелодии Шопена, Бетховена, Скрябина, что во многих творениях этих композиторов кульминация, как правило, приходится на слабую долю пятого, то есть на точку золотого сечения – 5/8. Л. Мазель считал, что практически у каждого композитора – приверженца гармонического стиля можно найти подобную музыкальную структуру: пять тактов подъёма и три такта спуска. Это говорит о том, что метод золотого сечения активно применялся композиторами сознательно либо бессознательно. Вероятно, такое структурное расположение кульминационных моментов придает музыкальному произведению гармоническое звучание и эмоциональную окраску.

Серьёзное исследование музыкальных произведений на предмет проявления в них золотой пропорции предпринял композитор и музыковед Л. Сабанеев. Он изучил около двух тысяч творений разных композиторов и пришёл к выводу, что примерно в 75% случаев золотое сечение присутствовало в музыкальном произведении хотя бы один раз. Самое большое количество произведений, в которых встречается золотая пропорция, он отмечал у таких композиторов, как Аренский (95%), Бетховен (97%), Гайдн (97%), Моцарт (91%), Скрябин (90%), Шопен (92%), Шуберт (91%). Наиболее пристально он исследовал этюды Шопена и пришёл к выводу, что золотое сечение было определено в 24 этюдах из 27. Только в трёх этюдах Шопена золотая пропорция не была обнаружена. Иногда структура музыкального произведения включала в себя одновременно и симметричность, и золотое сечение. Например, у Бетховена многие произведения делятся на симметричные части, и в каждой из них проявляется золотое сечение.

Итак, можно сказать, что наличие золотого сечения в музыкальном произведении является одним из критериев гармоничности музыкальной композиции.

Золотое сечение в музыке кратко. Золотое сечение в искусстве и музыке

Золотое сечение — это явление, обнаруживаемое в искусстве и уходящее корнями глубоко в природу. Пифагорейцы считали золотое сечение одним из главных центров своего учения о числовой гармонии мира. Греки обнаружили именно эту пропорцию в хорошо сложенном человеческом теле. Она радует глаз, будучи воплощенной в скульптуре и архитектурных ансамблях.

В эпоху Возрождения золотое сечение становится главным эстетическим принципом. Леонардо да Винчи, Рафаэль, Микеланджело, Тициан и другие художники этой эпохи используют его в композициях своих полотен.

В музыке также есть следы вездесущего золотого сечения. Если длину струны уменьшить вдвое, тон повысится на одну октаву. Уменьшению длины струны в отношении 3/2 и 4/3 будут соответствовать интервалы квинта и кварта. Благозвучные интервалы и аккорды имеют соотношение частот, близкое к числу Ф. Кульминация мелодии часто приходится на точку золотого сечения ее общей продолжительности.

Современные музыковеды выявили золотое сечение в произведениях Баха, Бетховена, Шопена. Ими было проанализировано множество музыкальных произведений от Баха до Шостаковича. Приблизительно 85% проведенных исследований соответствует золотому сечению. В выдающихся произведениях отношения метрических масштабов основных разделов музыкальной формы соответствуют золотому сечению с точностью до пятого или шестого знака. Кроме произведений крупной формы анализировались и миниатюры, например, прелюдии Скрябина, миниатюры Прокофьева, русские народные песни. Законы гармонии, законы золотого сечения были обнаружены и в этих произведениях.

На протяжении столетий звон колокола извещал людей об опасности, будил по утрам, указывал, когда наступило время отправляться на работу, садиться за трапезу и т.д. Колокольни — необходимая часть английского пейзажа. В континентальной Европе звонили сразу в несколько колоколов. Тот, кто правил колоколом, правил городом. Колокольному звону придавалось важное значение. Искусству колокольного звона мы обязаны не только мелодичным звучанием колоколов, но и обширной, детально разработанной терминологией, позволяющей звонарям обмениваться краткими и точными репликами во время исполнения переборов с вариациями.

Чтобы перезвонить все возможные вариации из восьми колоколов, потребовалось бы двадцать четыре часа. На семи колоколах все мыслимые ударные комбинации можно перезвонить за три с половиной часа.

Малый простой звон:

3 12546 32 1456 234 165 2436 1 5 42635 1 46253 1 6452 1 3 6 54 123 56 1432 5 16342 153624 135264

2 14365 24 1635 426 153 4625 13 64523 1 65432 1 5634 12 536 142 3 5 16 2 4 3 15264 132546

123456 312546

214365 321456

241635 234 165

426 153 2436 1 5

462513 426351

64523 1 46253 1

65432 1 6452 1 3

563412 6 54 123

536142 561432

351624 516342

315264 153624

132546 135264

Звонарю, управляющемуся со своей веревкой и не отрывающему глаз от веревок, ведущих к колоколам, которые должны пробить раньше или позже, приходится использовать симметрию: если звонарь остановит колокол слишком рано, то свободный конец веревки будет путаться под ногами и при обратном качании колокол не будет подниматься достаточно высоко. Если же звонарь потянет за веревку слишком сильно, то колокол может проскочить верхнюю точку и звонарь взлетит под потолок. Каким образом не искушенный в математике звонарь ощущает разницу между перестановками колоколов, остается загадкой, но именно это имеет решающее значение и в исполнении и в композиции звонов, древней и вечно живой разновидности искусства, радующих слух и восхищающих разум.

Гармония — это закон единства, она не может быть сведена к чистому количеству. Не случайно древние переносили законы музыкальной гармонии на всю Вселенную. Музыка, как и все искусство, выражает гармонию, но не количество, а качество, сущность, красоту, поэтому акценты следует перенести на описание качества.

Понимание гармонии как связи частей в целое исходит от искусства, а сама проблема гармонии возникла при сопоставлении законов восприятия с важнейшими фактами в искусстве, и особенно в музыке. Любое число можно преобразовать в любой далекий диапазон. Но перенос числа на семь октав имеет фундаментальный смысл, так как выражает границы качественной определенности чисел. В музыке семь октав: расстояние от самого нижнего звука до самого верхнего как раз равно семи октавам. Звуки ниже или выше наш слух уже не различает как качественно разные звуки. Но границы качественной определенности чисел связаны не только с семью октавами, а, по-видимому, вообще с числом семь: 7 звуков в гамме, 7 цветов в солнечном спектре, через 7 дней меняются фазы Луны, 7 дней в неделе, «7 дырок в голове» и т.д. Научный подвиг Д. Менделеева заключается в открытии им периодического закона, на основании которого он составил таблицу, названную впоследствии его именем и имеющую 7 периодов.

О роли числа 7 в Библии нет нужды говорить: это и 7 дней сотворения мира, 7 ангелов, 7 печатей, 7 светильников, 7 церквей и т.д. Можно предположить, что под числом 7 древние философы подразумевали некий высший принцип Бытия. В китайской системе счета четыре семерки распределялись между четырьмя Гениями, господствующими над четырьмя сторонами света.

Проанализировав бетховенскую «Апассионату», совершенство форм которой не вызывает сомнений, по количеству тактов в экспозиции, разбиению, репризе, ученые нашли там золотую пропорцию. Когда этот факт был обнаружен, он произвел впечатление «чуда», так как чем талантливее художник, тем точнее и разнообразнее работают числа. Потом золотая пропорция была выявлена в фортепьянной сонате № 4 Прокофьева.

Из всех искусств только музыка поддается точному численному анализу, поэтому она стала превосходным чувственным материалом, конкретным кодом, в котором зашифрованы законы гармонии мира. Все познание фактически представляет собой расшифровку труднейшего и сложнейшего кода и перевода его на язык науки. При этом можно с уверенностью сказать, что установленные законы лишь слегка приоткрывают занавес, за которым разворачивается целый океан событий, совершенно не познанных.

Видео Музыка Золотого Сечения "Голос издалека"

Золотое сечение в поэзии. Поэзия и золотое сечение

Раньше я писал о.
Вспомним числа ряда Фибоначчи: 0-1-1-2-3-5-8-13-21-34--55-89-144-233…(ряд бесконечный). Писал я и о том, что частные от деления чисел этого ряда на предыдущие монотонно приближаются к пропорции золотого сечения 1, 61803…
Продолжая эту тему, можно отметить, что даже в стихах выдающихся поэтов наблюдается следование этим закономерностям, хотя я не думаю, что они делали это сознательно. Скорее всего, "работала" высокая культура и обострённое ощущение прекрасного.
Многое в структуре поэтических произведений роднит этот вид искусства с музыкой. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Каждый стих обладает своей музыкальной формой - своей ритмикой и мелодией. Можно ожидать, что в строении стихотворений проявятся некоторые черты музыкальных произведений, закономерности музыкальной гармонии, а следовательно, и золотая пропорция.
Начнем с величины стихотворения, то есть количества строк в нем. Казалось бы, этот параметр стихотворения может изменяться произвольно. Однако оказалось, что это не так. Например, проведенный Н. Васютинским анализ стихотворений А.С. Пушкина с этой точки зрения показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи).
Многими исследователями было замечено, что стихотворения подобны музыкальным произведениям; в них также существуют кульминационные пункты, которые делят стихотворение в пропорции золотого сечения. Рассмотрим, например, стихотворение А.С. Пушкина "Сапожник":

Картину раз высматривал сапожник
И в обуви ошибку указал;
Взяв тотчас кисть, исправился художник,
Вот, подбочась, сапожник продолжал:
"Мне кажется, лицо немного криво …
А эта грудь не слишком ли нага?
Тут Апеллес прервал нетерпеливо:
"Суди, дружок, не выше сапога!"
Есть у меня приятель на примете:
Не ведаю, в каком бы он предмете
Был знатоком, хоть строг он на словах,
Но черт его несет судить о свете:
Попробуй он судить о сапогах!

Проведем анализ этой притчи. Стихотворение состоит из 13 строк. В нем выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 - числа Фибоначчи).
Одно из последних стихотворений Пушкина "Не дорого ценю я громкие права…" состоит из 21 строки и в нем выделяется две смысловые части: в 13 и 8 строк.

Не дорого ценю я громкие права,
От коих не одна кружится голова.
Я не ропщу о том, что отказали боги
Мне в сладкой участи оспаривать налоги
Или мешать царям друг с другом воевать;
Морочит олухов, иль чуткая цензура
В журнальных замыслах стесняет балагура.
Все это, видите ль, слова, слова, слова.
Иные, лучшие, мне дороги права:
Иная, лучшая, потребна мне свобода:
Зависеть от царя, зависеть от народа -
Не все ли нам равно? Бог с ними.
Никому
Отчета не давать, себе лишь самому
Служить и угождать; для власти, для ливреи
Не гнуть ни совести, ни помыслов, ни шеи;
По прихоти своей скитаться здесь и там,
Дивясь божественным природы красотам,
И пред созданьями искусств и вдохновенья
Трепеща радостно в восторгах умиленья,
Вот счастье! Вот права …

Характерно, что и первая часть этого стиха (13 строк) по смысловому содержанию делится на 8 и 5 строк, то есть все стихотворение построено по законам золотой пропорции.
Представляет несомненный интерес анализ романа "Евгений Онегин", сделанный Н. Васютинским. Этот роман состоит из 8 глав, в каждой из них в среднем около 50 стихов. Наиболее совершенной, наиболее отточенной и эмоционально насыщенной является восьмая глава.
Н. Васютинский констатирует:
"Кульминацией главы является объяснение Евгения в любви к Татьяне - строка "Бледнеть и гаснуть … вот блаженство!". Эта строка делит всю восьмую главу на две части - в первой 477 строк, а во второй - 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!".
Знаменитое стихотворение Лермонтова "Бородино" делится на две части: вступление, обращенное к рассказчику и занимающее лишь одну строфу ("Скажи- ка, дядя, ведь недаром…"), и главную часть, представляющее самостоятельное целое, которое распадается на две равносильные части. В первой из них описывается с нарастающим напряжением ожидание боя, во второй - бой с постепенным снижением напряжения к концу стихотворения. Граница между этими частями является кульминационной точкой произведения и приходится как раз на точку деления его золотым сечением.
Главная часть стихотворения состоит из 13 семистиший, то есть из 91 строки. Разделив ее золотым сечением (91:1,618 = 56,238), убеждаемся, что точка деления находится в начале 57-го стиха, где стоит короткая фраза: "Ну ж был денек!" . Именно эта фраза представляет собой "кульминационный пункт возбужденного ожидания", завершающей первую часть стихотворения (ожидание боя) и открывающий вторую его часть (описание боя).

Таким образом, золотое сечение играет в поэзии весьма осмысленную роль, выделяя кульминационный пункт стихотворения.
В молодости Леонардо отдал много сил и времени поискам математических закономерностей красоты. И, хотя в конце жизни он пришёл к идее непознаваемости мира, можно сказать, что он и другие выдающиеся деятели Возрождения внесли существенный вклад в решение этой задачи. Фундаментом их исследований была древнегреческая культура, которая тоже не возникла на пустом месте - она развивала достижения культуры древнего Египта и Востока, которые в конечном итоге опирались на достижения
.
Греческая культура, творчески обогатившая и развившая достижения Египта и Востока, явившаяся фундаментом европейской культуры, заслуживает отдельного разговора. Конечно, только на отдельных примерах - это огромная тема.

Золотое сечение в математике. Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

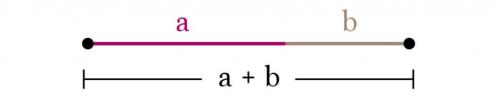
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

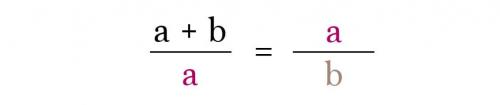
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.