"Парадокс Блондинки". Американский математик, нобелевский лауреат Джон Нэш учит ухаживать за девушками.

"Парадокс Блондинки". Американский математик, нобелевский лауреат Джон Нэш учит ухаживать за девушками.

Правила. Компания неженатых молодых людей вечер в баре проводит. Они замечают за соседним столиком компанию девушек - прекрасную блондинку и несколько менее симпатичных брюнеток и шатенок. Как начать за ними ухаживать?

История и применение "если мы все рванем к блондинке, то помешаем друг другу и она не достанется никому. Тогда мы займемся подружками, и они оттолкнут нас - никто не хочет быть вторым сортом. А вот если ее никто не заметит, мы не будем толкаться и не оскорбим других девушек. Так мы выиграем. Лишь так получим женщин. Адам Смит считал, что лучше всего, когда каждый член группы действует в своих интересах. Это правда, но не вся. На деле результат будет оптимальным, если каждый член группы сделает как лучше для себя и для группы "- это Цитата из Фильма"игры разума". Прототипом главного героя стал математик, нобелевский лауреат Джон Нэш, знаменитый тем, что сумел побороть симптомы шизофрении.

Неизвестно, была ли ситуация с блондинкой реальной, nо премию имени Нобеля Джон Нэш получил как раз за разработку теории игр. До него математики занимались в основном играми "с Нулевой Суммой" - это когда выигрыш равен проигрышу, блондинка достается либо одному, либо другому. Нэш занимался теми ситуациями, когда сумма не равна нулю, то есть кому-то достается брюнетка, кому-то - шатенка.

Нобелевку он получил за стратегию игры, которая сейчас называется "Равновесие по Нэшу". Энциклопедии описывают ее так: "Ситуация, в Которой ни Один Участник не Может Увеличить Выигрыш, Изменив Свое Решение в Одностороннем Порядке, Когда Другие Участники не Меняют Решения".

Понятное дело, что при знакомстве с барышнями в баре мало кто использует математику (если только вы - не будущий нобелевский лауреат. Зато эти формулы очень хорошо работают в бизнесе - собственно, премия досталась Нэшу именно в номинации "Экономика".
Человеческие качества. Бытовая мораль из трудов гениального математика очень проста: сотрудничать лучше, чем конкурировать.

Связанные вопросы и ответы:

Равновесие Нэша в экономике. Равновесие Нэша

Ученые стремились сформулировать основополагающие критерии рационального поведения участника на рынке с целью достижения благоприятных результатов. Они различали две основные категории игр. Первая - "игра с нулевой суммой", предусматривающий такой выигрыш, который состоит исключительно из проигрыша других игроков. В связи с этим пользу одних непременно должна образовываться за счет потерь других игроков, так что общая сумма пользы и потерь всегда равна нулю. Вторая категория - "игра с плюсовой суммой", когда индивидуальные игроки соревнуются за выигрыш, состоящий из их же ставок. Иногда он образуется за счет наличия "выходного" (термин из карточной игры в бридж, который означает одного из игроков, который, делая ставку, не участвует в игре), совсем пассивного и часто является служащим объектом эксплуатации. В обоих случаях игра неизбежно сопряжена с риском, поскольку каждый из ее участников, как считали исследователи, "стремится максимально повысить функцию, переменные которой ним не контролируются". Если все игроки являются умелыми, то решающим фактором становится случайность. Но так бывает редко. Почти всегда важную роль в игре играет хитрость, с помощью которой делаются попытки раскрыть замыслы противников и завуалировать свои намерения, а затем занять выгодные позиции, которые заставили бы этих противников действовать в ущерб самим себе. Многое зависит и от "контрхитрости".

Равновесие по нэшу. Равновесие Нэша

Равновесие Нэша – это часть теории игр, её автором выступил американский математик Джон Нэш. Эта теория демонстрирует оптимальную игру «в вакууме»: когда ставить олл-ин или коллировать пуш оппонентов. Важно понимать, что стратегия  пуша/колла по Нэшу в современных покерных реалиях уже не является единственно верной. Она является оптимальной только при условии, если ваши оппоненты знают об этой стратегии и придерживаются её без отклонений.

Оптимально использовать стратегию пуш/фолда по Нэшу можно только против сильных и понимающих игроков. При минимальном отклонении эффективность этой стратегии значительно снижается. Наиболее выгодным вариантом использования равновесия Нэша является подстройка под оппонентов, и коррекция собственной игры на основе диапазонов соперников.

Где использовать равновесие Нэша?

Диапазоны равновесие Нэша подходят для игры в МТТ , Sit&Go и турнирах Spin&Go . Применять эту стратегию следуют, когда ваш стек опускается до 15 больших блайндов или ниже, и ваша игра сводится к одним пуш/фолд решениям. Чтобы отточить свое мастерство игры, вам следует использовать специальное программное обеспечение, которое моделирует такие ситуации: SNGWizard и ICMIZER.

Предположим, что ваш оппонент идет олл-ин, а у вас осталось 14 больших блайндов. По равновесию Нэша, вы можете коллировать с широким диапазоном рук, имея 20 BB, включая карманные тройки, QJ, QT и даже K2s.

Но это диапазон «в вакууме», который не учитывает тип турнира, стадию и разницу в выплатах. Эта стратегия является математически верной, но только при условии, что игра состоит только из двух решений префлоп: пуш или фолд. В современных реалиях сильные игроки способны сыграть глубокую постфлоп раздачу и со стеком в 15 больших блайндов.

Помимо использования равновесия Нэша, вы всегда можете просто подождать хорошей руки и заколлировать противника. Но если вы точно не знаете, что является хорошей рукой относительно размера вашего стека, то ориентируйтесь на таблицы Нэша.

Диапазон пуша Нэшу

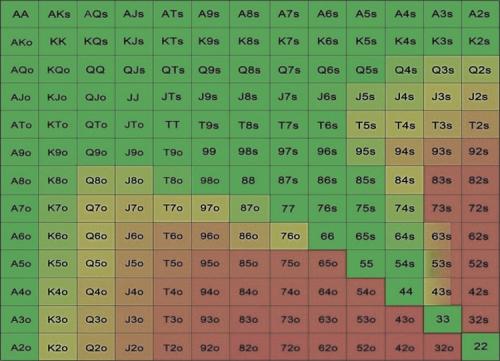
Диапазон колла по Нэшу

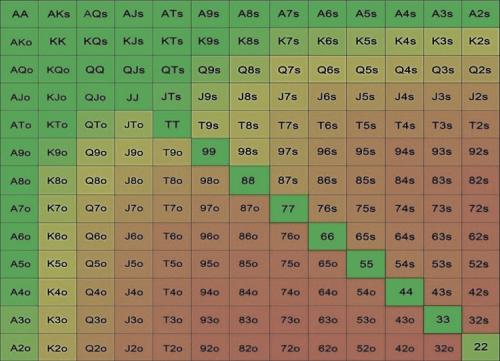
Зеленый цвет – эффективный стек от 15 до 20 больших блайндов.

Желтый и темно-желтый цвет – эффективный стек от 6 до 14 больших блайндов.

Красный цвет – эффективный стек от 1 до 5 больших блайндов.

Использование в своей игре равновесия Нэша подойдет начинающим  игрокам, поскольку предоставит первоначальное понимание о диапазонах пуша или колла для стандартных турнирных ситуаций и поможет достаточно быстро начать зарабатывать покером.

Равновесие нэша теория игр.

Эта относительно молодая ветвь математики была создана в 1930е годы Джоном фон Нейманом и Оскаром Моргеншетрном. Фон Нейман был замечательным математиком, и практически в одиночку создал теорию информации и теорию игр. Его исследования во многом поспособствовали развитию вычислительной техники и появлению компьютера. Позже, в 1950-е годы большую роль в развитие теории игр внес американский математик, лауреат Нобелевской премии по экономике, Джон Нэш . История жизни Джона Нэша настолько необычна, что легла в основу фильма «Игры разума» 2001 года. В школе Нэш не любил математику, поскольку ее преподавали посредственно. Но в 14 лет к нему в руки попала книга «Творцы математики» Эрика Белла, после прочтения которой он смог доказать малую теорему Ферма. Чуть позже Нэш наткнулся на труды фон Неймана и Моргенштерна, и в 21 год он написал диссертацию по теории игр. Именно за эту работу он получил в 1994 году Нобелевскую премию по экономике.

Теория игр (game theory) изучает, каким образом выстраивают свое поведение агенты в так называемых «играх» - ситуациях, когда результат принятия решений зависит не только от поведения данного агента, но и от поведения других участников игры.
Индивид, принимая решения, может догадываться о том, как будут вести себя другие участники игры. Индивид будет принимать решение исходя из рациональной догадки о поведении других. Говорят, что в этом случае индивид следует определённой игровой стратегии.

Игровая стратегия – это линия поведения участника в зависимости от предположений об ответных действиях других участников. Доминирующая игровая стратегия – это стратегия, при которой участник получает максимальный выигрыш при любых действиях других сторон.
Что такое игровая стратегия и доминирующая игровая стратегия лучше всего показать на конкретном примере – простейшей игре под названием «дилемма заключенного», анализ которой и положил начало теории игр.

Дилемма заключенного - это игра между двумя участниками с двумя возможными исходами и одновременными ходами.

Суть игры заключается в следующем. Представьте, что вы с напарником совершили преступление, например, ограбили банк. Полиция поймала вас обоих и теперь проводит допрос каждого из них в разных камерах. Полиция предлагает вам сделку: вы даете показания на своего напарника, и тогда выходите на свободу. Такую же сделку предлагают вашему напарнику.
Каждый из преступников имеет выбор: давать показания на напарника или молчать. Если вы оба даете показания друг на друга, то каждый получает по 2 года тюрьмы. Если вы оба молчите, то в полной мере вашу вину будет трудно доказать, и каждый получит только по 1 году. Но если вы даете показания на вашего подельника, а он нет, то вы выходите на свободу, а ваш подельник получает 5 лет тюрьмы.
Таким образом, приговор, который получит каждый преступник, зависит не только от его показаний, но и от показаний другого преступника.

Парадоксы теории игр. Парадокс Паррондо

Парадокс Паррондо — парадокс в теории игр, который обычно характеризуют как проигрышную стратегию, которая выигрывает. Парадокс назван в честь его создателя, Хуана Паррондо, испанского физика. Утверждение парадокса выглядит следующим образом: Возможно выиграть, играя поочерёдно в две заведомо проигрышные игры.

1 

Парадокс заключается в следующем: играя в две специально подобранные игры А и Б, каждая из которых имеет более высокую вероятность проигрыша, чем победы, можно построить выигрышную стратегию, играя в эти игры поочерёдно. То есть, играя в одну игру, в которой на 5 проигрышей выпадает 4 выигрыша, игрок неизбежно проиграет по итогам большого количества розыгрышей. Затем, играя в другую, в которой на 10 проигрышей выпадает 9 выигрышей, игрок также проиграет. Но если чередовать эти игры, например АББАББ и т. п., то общая вероятность выигрыша будет больше вероятности проигрыша.

Условием возникновения парадокса Паррондо является связь между результатами игр А и Б. Вот пример:

===Вариант с капиталом игрока===

Связь двух игр может осуществляться через текущий капитал игрока. Пусть игра А такова, что игрок выигрывает 1€ с вероятностью 50 % — ? (с положительным, достаточно малым ?) и проигрывает 1€ с вероятностью 50 % + ? Математическое ожидание результата такой игры, очевидно, равняется –2?, то есть отрицательно. Игра Б является комбинацией двух игр — Б1 и Б2. Если капитал игрока в начале игры Б кратен 3, то он играет в Б1, иначе — в Б2. Игра Б1: игрок выигрывает 1€ с вероятностью 10 % — ?, проигрывает с вероятностью 90 % + ? Игра Б2: игрок выигрывает 1€ с вероятностью 75 % — ?, проигрывает с вероятностью 25 % + ? При некоторых значениях ? игра Б также обладает отрицательным ожиданием результата (например, при ? = 0,005). Можно видеть, что некоторые комбинации игр А и Б обладают положительным ожиданием результата. Например (с указанным значением ?): Случайно выбирая каждый раз игру между А и Б, мы получим ожидание результата 0,0147.

Играя поочерёдно 2 раза А, затем 2 раза Б, получаем ожидание результата 0,0148.

===Вариант с блокировкой игры===

Связь может также осуществляться ссылкой правил на общий предмет. Пусть перед игроком имеется жетон с двумя сторонами — белой и чёрной. Игра А: игрок бросает монетку: если жетон обращён белой стороной к игроку если выпал «орёл», то игрок получает 3€ если выпала «решка», то игрок теряет 1€ и переворачивает жетон другой стороной если жетон обращён чёрной стороной к игроку если выпал «орёл», то игрок получает 1€ если выпала «решка», то игрок теряет 2€ Игра Б: игрок бросает монетку: если жетон обращён чёрной стороной к игроку если выпал «орёл», то игрок получает 3€ если выпала «решка», то игрок теряет 1€ и переворачивает жетон другой стороной если жетон обращён чёрной стороной к игроку если выпал «орёл», то игрок получает 1€ если выпала «решка», то игрок теряет 2€

Очевидно, что играя в одну из этих игр, игрок в среднем будет проигрывать, играя же в эти игры поочерёдно (или каждый раз выбирая случайным образом одну из двух игр), игрок получает возможность выбраться из неблагополучной для него конфигурации.

Вы поняли ? Я не особо

---

---

Определить равновесие по нэшу. Биматричные игры В играх с

Пример №1 . Борьба за рынки сбыта.
Фирмаанамерена сбыть партию товара на одном из двух рынков, контролируемых более крупной фирмойb. С этой целью она проводит подготовительную работу, связанную с определенными затратами. Если фирмаbразгадает, на каком из рынков фирмаабудет продавать свой товар, она примет контрмеры и воспрепятствует "захвату" рынка (этот вариант означает поражение фирмыа); если нет, то фирмааодерживает победу. Предположим, что для фирмыапроникновение на первый рынок более выгодно, чем проникновение на второй, но и борьба на первом рынке требует от нее больших средств. Например, победа фирмыана первом рынке приносит ей вдвое большую прибыль, чем победа на втором, но зато поражение на первом рынке полностью ее разоряет.
Составим математическую модель этого конфликта, считая фирмуаигроком 1 и фирмуbигроком 2. Стратегии игрока 1: А 1– проникновение на рынок 1, А 2– проникновение на рынок 2; стратегии игрока 2: В 1– контрмеры на рынке 1, В 2– контрмеры на рынке 2. Пусть для фирмыаее победа на 1-м рынке оценивается в 2 единицы, а победа на 2-м рынке – в 1 единицу; поражение фирмыана 1-м рынке оценивается в -10, а на 2-м в -1. Для фирмыbее победа составляет соответственно 5 и 1 единицу, а поражение -2 и -1. Получаем в итоге биматричную игруГс матрицами выигрышей
.
По теореме эта игра может иметь либо чистые, либо вполне смешанные ситуации равновесия. Ситуаций равновесия в чистых стратегиях здесь нет. Убедимся теперь, что данная игра имеет вполне смешанную ситуацию равновесия. Находим,.
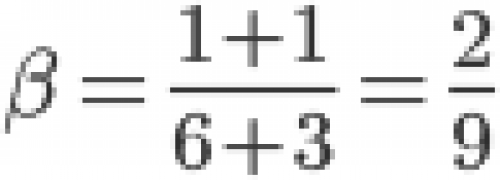Итак, рассматриваемая игра имеет единственную ситуацию равновесия, где,. Она может быть реализована при многократном повторении игры (то есть при многократном воспроизведении описанной ситуации) следующим образом: фирмаадолжна использовать чистые стратегии 1 и 2 с частотами 2/9 и 7/9, а фирмаb– чистые стратегии 1 и 2 с частотами 3/14 и 11/14. Любая из фирм, отклонившись от указанной смешанной стратегии, уменьшает свой ожидаемый выигрыш.

Парадокс блондинки в экономике.

«Парадокс блондинки»: как нобелевский лауреат Джон Нэш учил ухаживать за девушками

Правила Компания неженатых молодых людей проводит вечер в баре. Они замечают за соседним столиком компанию девушек — прекрасную блондинку и несколько менее симпатичных брюнеток и шатенок. Как начать за ними ухаживать?

История и применение «Если мы все рванем к блондинке, то помешаем друг другу и она не достанется никому. Тогда мы займемся подружками, и они оттолкнут нас — никто не хочет быть вторым сортом. А вот если ее никто не заметит, мы не будем толкаться и не оскорбим других девушек. Так мы выиграем. Лишь так получим женщин. Адам Смит считал, что лучше всего, когда каждый член группы действует в своих интересах. Это правда, но не вся. На деле результат будет оптимальным, если каждый член группы сделает как лучше для себя и для группы» — это цитата из фильма «Игры разума». Прототипом главного героя стал математик, нобелевский лауреат Джон Нэш, знаменитый тем, что сумел побороть симптомы шизофрении.

Неизвестно, была ли ситуация с блондинкой реальной. Но премию имени Нобеля Джон Нэш получил как раз за разработку теории игр. До него математики занимались в основном играми «с нулевой суммой» — это когда выигрыш равен проигрышу, блондинка достается либо одному, либо другому. Нэш занимался теми ситуациями, когда сумма не равна нулю, то есть кому-то достается брюнетка, кому-то — шатенка.

Нобелевку он получил за стратегию игры, которая сейчас называется «равновесие по Нэшу». Энциклопедии описывают ее так: «Ситуация, в которой ни один участник не может увеличить выигрыш, изменив свое решение в одностороннем порядке, когда другие участники не меняют решения».

Понятное дело, что при знакомстве с барышнями в баре мало кто использует математику (если только вы не будущий нобелевский лауреат). Зато эти формулы очень хорошо работают в бизнесе — собственно, премия досталась Нэшу именно в номинации «Экономика».

Парадокс блондинки википедия. Парадокс Денни

Материал из Википедии — свободной энциклопедии

Парадо́кс Де́нни ( англ.   Denny’s paradox ), в исследовании локомоции  — кажущаяся невозможность для живущих на поверхности воды животных (например, водомерок ) приложения достаточной для перемещения силы . Парадокс назван в честь Марка Дэнни , профессора биологии Стэнфордского университета .

Если предполагается, что передачу импульса воде производят поверхностные волны, то ноги животного должны перемещаться быстрее, чем фазовая скорость волн cm=(4gσ/ρ)1/2{\displaystyle c_{m}=(4g\sigma /\rho )^{1/2}} , где g  — ускорение свободного падения , σ — коэффициент поверхностного натяжения , и ρ — плотность воды. Для стандартных условий эта скорость равна примерно 0,23 м/с.

Движение ножек молодых водомерок гораздо медленнее, чем приведённая выше скорость, и поэтому они не могут перемещаться.

Дэвид Ху и Джон Буш утверждают, что парадокс Денни

…основывался на двух некорректных предположениях. Во-первых, предполагалось, что движение водомерок основано на возбуждении поверхностных волн, так как считалось, что движущая сила связана с волновым сопротивлением, действующим на приводящую ногу. Во-вторых, предполагалось, что для возбуждения поверхностных волн скорость ноги водомерки должна превышать минимальную скорость волн cm=(4gσ/ρ)1/2≃0,23{\displaystyle c_{m}=\left(4g\sigma /\rho \right)^{1/2}\simeq 0{,}23} м/с. Отметим, что второе предположение строго справедливо только для установившегося движения.

Оригинальный текст  (англ.)

…rested on two flawed assumptions. First, water striders' motion was assumed to rely on the generation of capillary waves, since the propulsive force was thought to be that associated with wave drag on the driving leg. Second, in order to generate capillary waves, it was assumed that the strider leg speed must exceed the minimum wave speed, cm=(4gσ/ρ)1/2≃0.23{\displaystyle c_{m}=\left(4g\sigma /\rho \right)^{1/2}\simeq 0.23} m/s. We note that this second assumption is strictly true only for steady motions.

— David L. Hu, John W. M. Bush. «The hydrodynamics of water-walking arthropods»